Möller–Trumbore Intersection algorithm

This algorithm can efficiently detect and ccompute the intersections of a ray q through a face p. Each ray is defined in 3-space as the trajectory from $q_1$ to $q_2$ such that our general ray matrix q with shape $[2 \times 3 \times \rm{nr}]$ is defined by such:

\[q_k =\begin{bmatrix}q_1\\q_2\end{bmatrix}_k = \begin{bmatrix} q_{1,x} & q_{1,y} & q_{1,y} \\ q_{2,x} & q_{2,y} & q_{2,z} \\ \end{bmatrix}_k\]

The faces p are defined by the 3 vertices in 3-space with shape $[3 \times 3 \times \rm{nt}]$:

\[p_k = \begin{bmatrix}p_1\\p_2\\p_3\end{bmatrix}_k = \begin{bmatrix} p_{1,x} & p_{1,y} & p_{1,z} \\ p_{2,x} & p_{2,y} & p_{2,z} \\ p_{3,x} & p_{3,y} & p_{3,z} \\ \end{bmatrix}_k\]

The interaction between a ray and a face can be defined as intersecting and non-intersecting:

The volume of a tetrahedron is defined by:

\[\boxed{V(a, b, c, d) = \frac{(d-a) \cdot ((b-a) \times (c-a))}{6}}\]

Therefore, the signed volumes are can be defined by:

\[\begin{aligned} s_1 = \text{sgn } V(q_1, p_1, p_2, p_3)\\ s_2 = \text{sgn }V(q_2, p_1, p_2, p_3)\\ s_3 = \text{sgn }V(q_1, q_2, p_1, p_2)\\ s_4 = \text{sgn }V(q_1, q_2, p_2, p_3)\\ s_5 = \text{sgn }V(q_1, q_2, p_3, p_1)\\ \end{aligned}\]

Where $V(r_1, r_2, r_3, r_4)$ is the signed volume of the tetrahedron defined by r.

And intersection exists if:

\[s_1 \neq s_2 \quad \& \quad s_3 = s_4 \quad \& \quad s_4 = s_5\]

It is implied by $s_1 \neq s_2$ that $q_1$ and $q_2$ lay on opposite sides of $p_k$

in which case the intersection point $q_0$ is then given by:

\[q_0 = q_1 + t (q_2-q_1)\]

where:

\[n = (p_2-p_1) \times (p_3-p_1)\] \[t = \frac{(p_1-q_1) \cdot n}{(q_2-q_1) \cdot n}\]

Examples

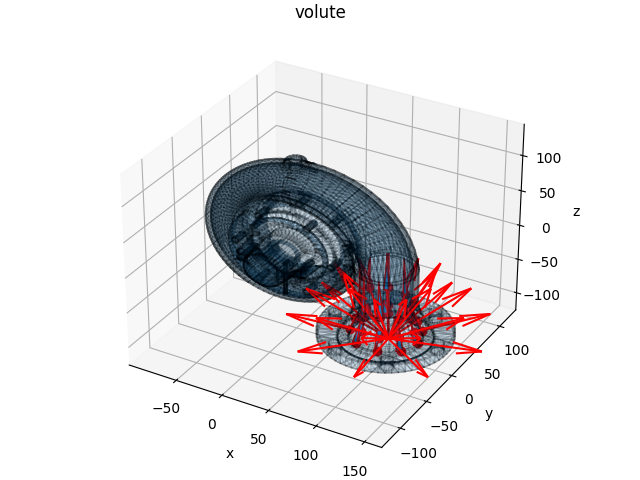
Spherical Shell

And example of the algorithm tracing through a spherical shell can be realized as follows:

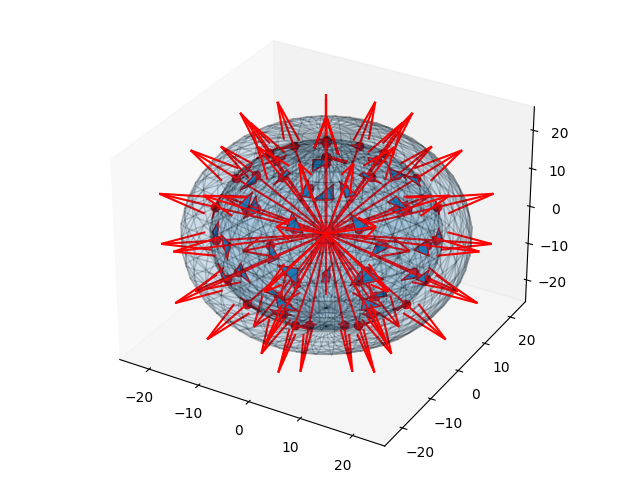
We can also apply to more complicated shapes